Don’t like maths? Stop reading now!
To add any real challenge, my basketball simulation requires modelling the motion of a basketball using principles from physics, particularly Newtonian mechanics, incorporating gravity, air resistance (drag), and collisions with the floor, backboard, and rim (hoop).
The Inputs
When throwing a ball, a few factors are crucial:
- Gravity (g): The acceleration due to gravity, is approximately 9.8 m/s2.
- Initial velocity (v0): The speed at which the ball is thrown.
- Angle of release (θ): The angle to the horizontal.
- Height of release (h0): The height above the ground from which the ball is thrown.
Equations of Motion
The basic motion of the ball can be separated into two components: horizontal and vertical.
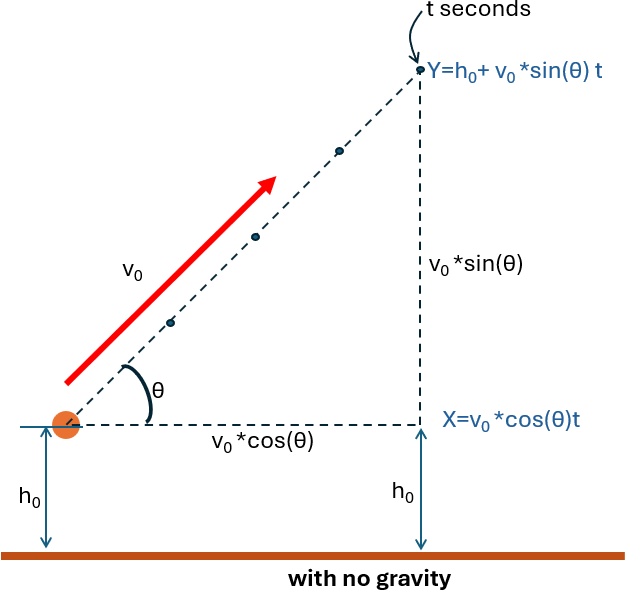
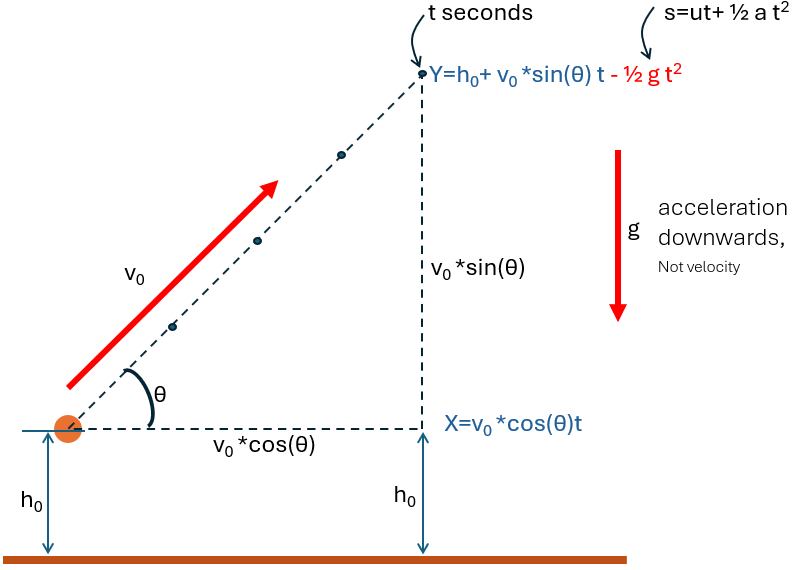
But unless we want our ball going upwards to space, we need to apply a force downward aka gravity:
Horizontal Motion
x(t)=v0⋅cos(θ)⋅t
- x(t): Horizontal position after time t.
- v0⋅cos(θ): Horizontal component of the velocity (constant, as no horizontal forces act in ideal cases).
Vertical Motion
y(t)=h0+v0⋅sin(θ)⋅t−0.5gt2
- y(t): Vertical position after time t.
- v0⋅sin(θ): Initial vertical velocity component.
- −0.5gt2: Effect of gravity over time.
The motion was described simply enough, but it’s missing something. Where does throwing come into it, and how did it acquire velocity v0?
The force you exert on the ball during the throw determines its initial velocity, and this process involves Newton’s second law (F=ma) applied whilst the time the ball is in your hand. However, when we analyze the projectile motion of the ball after it leaves your hand, we simplify the problem by focusing on the ball’s state at the moment of release, characterized by its initial velocity (v0) and launch angle (θ). It’s a simplification but generally accurate.
We have focused on the X & Y position of the ball, because ultimately that matters. But what happens to velocity?
Air resistance, collision and friction result in horizontal velocity reduction. Vertically, were it not for the same factors plus gravity the ball would end up going into space. With gravity the velocity is reduced (slows down in the upwards direction) until eventually reaching 0 velocity, followed by accelerating downward.
Without the factors that slow the ball, the prediction of the correct force would be quite simple. However because they depend on the speed, we can’t do that – we have to do it step by step.
Force and Acceleration Before Release
The interaction between your hand and the ball involves:
- Force: The force F you exert depends on the strength of your throw.
- Mass: For a heavier ball, the same force produces less acceleration (a=F/m).
- Time: The ball is in contact with your hand for a short duration (tcontact), accelerating from rest to its release velocity.
The final velocity at the moment of release is:
v0=a⋅tcontact=(F/m)⋅tcontact
Why do we focus on v0 instead of force F?
Once the ball leaves your hand, you no longer apply force on it (ignoring air resistance). Its motion from that point is entirely determined by its velocity, angle, and external forces like gravity. By solving for v0 during the throw, we can shift to the simpler kinematic analysis for projectile motion.
In most practical cases, it is accurate enough:
- Neglecting Non-Linear Force Profiles: The force you exert may not be constant; it might increase as your muscles engage or follow a specific curve. However, as long as we focus on the resulting v0, this complexity is encapsulated in that single value.
- Short Throw Duration: The hand-ball interaction happens over a very short time (milliseconds to fractions of a second). The details of how F varies during this time don’t significantly affect the motion after release, provided v0 is accurately calculated or measured.
The simplification to projectile motion assumes:
- Force is no longer acting: True after the ball leaves your hand.
- Initial velocity dominates: For typical throws, yes.
It won’t work for…
- Heavy objects (shotput): A lower v0 results due to high mass and short tcontact.
- Complex dynamics during the throw: For example, in javelin throwing, where the angle and velocity change due to flex and drag during the throw itself.
If you want to consider the force applied during the throw explicitly:
- Assume you exert a constant or variable force over a distance (s) while accelerating the ball.
- Work-energy theorem: The work done on the ball translates to kinetic energy at release:
- F⋅s=0.5mv02
- v0=Sqrt(2F⋅s/m)
Alternatively, you can use F=ma and solve:
- v0=u+at=Fm⋅tcontact.
- v0 becomes the bridge between the force-based phase (throwing) and the kinematics phase (projectile motion).
Drag Force Equation
We also have “air resistance” as an added challenge. There is a standard formula for it:
- F = 1/2 * Cd * rho * A * v * v
Where:
- Cd is the drag coefficient
- rho is the air density
- A is the cross-sectional area of the ball.
- v is the speed of the ball.
The drag acceleration is calculated by rearranging F=ma to give a = F/M (F = drag, m=mass of ball).
We then applying v=u+at, where v=current velocity, and a = drag, t = time step and we have accurate-ish motion
This all sounds long-winded but fairly straightforward. That doesn’t mean it’s simple to solve.
These kinds of problems invariably rely on Euler’s numerical integration to update the ball’s position and velocity iteratively.
What does that mean?
We aren’t able to start a position x,y throw a ball at angle θ and know the correct force.
Why?
Because from the moment of launch, the ball speed slows due to drag and the drag depends on the speed.
Any super clever people out there are welcome to correct me.
The simulation uses real-world values for constants and measurements:
- Ball Properties:
- Radius: 0.121m
- Mass: 0.623kg
- Court Dimensions:
- Hoop Height: 3.05m
- Rim Radius: 0.2286m
- Coefficients:
- Gravity: 9.81m/s2
- Air Density: 1.225 kg/m3
- Drag Coefficient: 0.47
- Coefficient of Restitution: 0.6
